
Calon guru belajar matematika dasar SMP lewat soal dan pembahasan kesebangunan dan kekongruenan pada matematika SMP. Apa yang diharapkan setelah mempelajari materi ini, yaitu dapat menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar.
Soal matematika dasar kesebangunan dan kekongruenan untuk SMP kita pilih dari soal-soal yang sudah pernah diujikan pada soal Ujian Sekolah matematika SMP, soal Ujian Nasional matematika SMP, atau soal ujian seleksi akademik masuk SMA Unggulan atau SMA Plus.
KESEBANGUNAN
Dua buah bangun dikatakan sebangun (kecuali lingkaran) apabila:
- Besar sudut yang seletak atau bersesuaian sama besar.
- Perbandingan panang sisi yang seletak atau bersesuaian adalah sebanding.
Sebangun disimbolkan dengan $\sim$, misalkan $\bigtriangleup ABC$ sebangun dengan $\bigtriangleup PQR$ dapat dituliskan dengan $\bigtriangleup ABC \sim \bigtriangleup PQR$.

Akibat dari kesebangunan maka diperoleh perbandingan sisi-sisi yang bersesuaian sama besar. Jika kita gunakan segitiga di atas sebagai pedoman, maka kita peroleh;
\begin{align} \dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{AC}{PR} \end{align}
KEKONGRUENAN
Dua buah bangun dikatakan kongruen apabila:
- Besar sudut yang seletak atau bersesuaian sama besar.
- Panjang sisi yang seletak atau bersesuaian ukurannya sama.
Dengan kata lain dua bangun dikatakan kongruen jika ukuran dan bentuknya sama. Kongruen disimbolkan dengan $\cong$, misalkan $\bigtriangleup ABC$ kongruen dengan $\bigtriangleup PQR$ dapat dituliskan dengan $\bigtriangleup ABC \cong \bigtriangleup PQR$.

CIRI-CIRI DUA SEGITIGA KONGRUEN
Dua buah segitiga dapat dikatakan kongruen jika dipenuhi salah satu dari ciri berikut ini:
- Panjang sisi-sisi kedua segitiga adalah sama. Dapat diingat dengan ciri "sisi-sisi-sisi".
- Dua sisi segitiga yang bersesuaian mempunyai ukuran yang sama dan membentuk sudut yang sama besar. Dapat diingat dengan ciri "sisi-sudut-sisi".
- Dua sudut segitiga yang bersesuaian sama besar dan sisi yang letaknya diantara kedua sudut sama ukurannya sama. Dapat diingat dengan ciri "sudut-sisi-sudut".
SOAL LATIHAN dan PEMBAHASAN MATEMATIKA SMP
1. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Pada gambar berikut, segitiga $PQR$ dan segitiga $STU$ merupakan sua segitiga kongruen. Besar $\angle R=\angle U$ dan $\angle Q=\angle S$. Manakah pasangan sisi yang sama panjang?
Besar sudut $BAC$ adalah...
$\begin{align}
(A)\ & PR=SU \\
(B)\ & QR=TU \\
(C)\ & PQ=SU \\
(D)\ & PQ=ST
\end{align}$
Alternatif Pembahasan:
Jika kita gambrakan dengan menambahkan informasi yang ada pada soal, maka gambar segitiga akan tampak seperti berikut ini:

- $\angle R=\angle U$, $\angle Q=\angle S$, $\angle P=\angle T$
- $PR=TU$, $PQ=TS$, dan $QR=US$
$\therefore$ Pilihan yang sesuai adalah $(D)\ PQ=ST$
2. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Sebuah pohon yang berada di depan gedung mempunyai tinggi $8\ m$. Pada saat yang sama bayangan gedung berimpit dengan bayangan pohon seperti tampak pada gambar di bawah.
Tinggi gedung yang sesuai ukuran tersebut adalah....
$\begin{align}
(A)\ & 5,30\ m \\
(B)\ & 6,25\ m \\
(C)\ & 10,00\ m \\
(D)\ & 12,00\ m
\end{align}$
Alternatif Pembahasan:
Jika kita misalkan titik-titik penting pada gambar kita beri nama seperti berikut ini;

$\begin{align}
\dfrac{AB}{AD} &= \dfrac{BC}{DE} \\
\dfrac{10}{15} &= \dfrac{8}{DE} \\
DE &= \dfrac{8 \times 15}{10} \\
DE &= 12
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 12,00\ m$
3. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Perhatikan Tabel| Klub | Menang | Seri | Kalah |
| Man United | $28$ | $7$ | $3$ |
| Arsenal | $22$ | $7$ | $9$ |
| Leeds United | $21$ | $6$ | $11$ |
| Liverpool | $19$ | $10$ | $9$ |
| Chelsea | $18$ | $11$ | $9$ |
Untuk setiap hasil pertandingan diberi nilai seperti berikut ini:
| Hasil | Nilai |
| Menang | $3$ |
| Seri | $1$ |
| Kalah | $0$ |
4. Soal UNBK Matematika SMP 2019 |*Soal Lengkap
Perhatikan gambar
Seseorang akan mengukur lebar sungai dengan cara menancapkan tongkat $A,B,C, \text{dan}\ D$ seperti pada gambar. Tongkat $A$ segaris dengan pohon $E$ diseberang sungai. Jika $AB=12\ m$, $BD=15\ m$ dan $CD=25\ m$, lebar sungai adalah...
$\begin{align}
(A)\ & 15\ m \\
(B)\ & 20\ m \\
(C)\ & 31\ m \\
(D)\ & 35\ m
\end{align}$
Alternatif Pembahasan:
Dari gambar di atas, $\bigtriangleup ABE$ sebangun dengan $\bigtriangleup BCD$ karena $\angle BAE=\angle BDC$ dan $\angle ABE=\angle CBD$, sehingga berlaku:
$\begin{align}
\dfrac{AB}{BD} &= \dfrac{AE}{CD} \\
\dfrac{12}{15} &= \dfrac{AE}{25} \\
\dfrac{4}{5} \times 25 &= AE \\
20 &= AE
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ 20\ m $
5. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap
Pada gambar berikut, segitiga $KLM$ kkongruen dengan segitiga $RST$.
Pernyataan yang sama panjang adalah...
$\begin{align}
(A)\ & KL+ST \\
(B)\ & LM=RS \\
(C)\ & KM=RT \\
(D)\ & KL=RT
\end{align}$
Alternatif Pembahasan:
Segitiga $KLM$ dan $RST$ kongruen, maka:
- $\angle K=\angle R=75^{\circ}$
- $\angle L=\angle S=35^{\circ}$
- $\angle M=\angle T=70^{\circ}$
- $KM=RT$
- $ML=TS$
- $KL=RS$
6. Soal Simulasi UNBK Matematika SMP 2019 |*Soal Lengkap
Perhatikan gambar berikut!
Jika $AB = BC = CD$. maka panjang $BF$ adalah...
$\begin{align}
(A)\ & 4\ cm \\
(B)\ & 4,5\ cm \\
(C)\ & 5\ cm \\
(D)\ & 5,5\ cm
\end{align}$
Alternatif Pembahasan:
Pada gambar ada simbol arah tanda panah, garis yang ada arah tanda panah artinya adalah garis yang sejajar.
Garis $AB$ sejajar dengan garis $CD$ dan garis $CB$ sejajar dengan garis $ED$.
Untuk mendapatkan panjang garis $BF$, kita coba gunakan garis bantu, ilustrasinya kurang lebih seperti berikut ini;
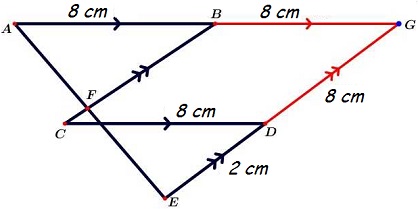
$\begin{align}
\frac{BF}{GE} & = \frac{AB}{AG} \\
\frac{BF}{10} & = \frac{7}{14} \\
BF & = \frac{1}{2} \times 10 \\
BF & = 5
\end{align}$
$\therefore$ Panjang $BF$ adalah $(C)\ 5\ cm$
7. Soal UNBK Matematika SMP 2018 |*Soal Lengkap
Perhatikan persamaan berikut!
$5(2x – 3) + 4 = 2(3x + 1) – (-3)$ mempunyai penyelesaian $n$. Nilai dari $3n + 5$ adalah...
$\begin{align}
(A)\ & 4 \\
(B)\ & 7 \\
(C)\ & 13 \\
(D)\ & 17
\end{align}$
Alternatif Pembahasan:
$\begin{align}
5(2x – 3) + 4 & = 2(3x + 1) – (-3) \\
10x – 15 + 4 & = 6x + 2 +3 \\
10x – 11 & = 6x + 5 \\
4x & = 16 \\
x & = \frac{16}{4}=4 \\
n & = 4 \\
3n + 5 & = 3(4)+1\\
& = 12+1=13
\end{align}$
$\therefore$ Nilai dari $2n + 1$ adalah $(C)\ 13$
8. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap
Perhatikan gambar berikut!
Sebidang tanah berbentuk trapesium samakaki. Di bagian dalam akan dibuat kolam ikan yang sebangun dengan tanah tersebut. Di sekeliling kolam dibangun jalan setapak. Luas jalan tersebut adalah...
$\begin{align}
(A)\ & 216\ m^{2} \\ (B)\ & 226\ m^{2} \\ (C)\ & 236\ m^{2} \\ (D)\ & 316\ m^{2}
\end{align}$
Alternatif Pembahasan:
Untuk menghitung luas jalan, kita coba menghitung dari selisih luas tanah dan luas kolam. Tanah dan kolam sama-sama berbentuk trapesium sama kaki, hanya ukurannya yang berbeda.

$\frac{x}{15}=\frac{36}{y}=\frac{20}{25}$
$\frac{x}{15}=\frac{36}{y}=\frac{4}{5}$
$\frac{x}{15}=\frac{4}{5}$
$x=\frac{4}{5} \times 15$
$x=12$
$\frac{36}{y}=\frac{4}{5}$
$y=\frac{5}{4} \times 36$
$y=45$
Luas trapesium adalah jumlah panjang garis sejajar dikali jarak dua garis sejajar lalu dibagi dua.

$d_{k}=\sqrt{20^{2}-12^{2}}$
$d_{k}=\sqrt{400-144}=16$
$d_{t}=\sqrt{25^{2}-15^{2}}$
$d_{t}=\sqrt{625-225}=20$
Luas kolam
$L_{k}=\frac{1}{2} \times (12+36) \times 16$
$L_{k}=\frac{1}{2} \times 48 \times 16$
$L_{k}=384$
Luas tanah
$L_{k}=\frac{1}{2} \times (15+45) \times 20$
$L_{k}=\frac{1}{2} \times 60 \times 20$
$L_{k}=600$
Luas jalan=Luas tanah-luas kolam
Luas jalan$=600-384=216\ m^{2}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 216\ m^{2}$
9. Soal Simulasi UNBK Matematika SMP 2018 |*Soal Lengkap
"Lebar Sungai"
Andi ingin mengetahui lebar sungai. Di seberang sungai terdapat sebuah pohon. Untuk itu dia menancapkan tongkat pada posisi A, B, C, dan D dengan ukuran seperti gambar.
Andi ingin mengukur lebar sungai dari tongkat D sampai pohon. Berapa lebar sungai tersebut?
$\begin{align}
(A)\ & 11\ m \\ (B)\ & 12\ m \\ (C)\ & 15\ m \\ (D)\ & 16\ m
\end{align}$
Alternatif Pembahasan:
Untuk menghitung lebar sungai dengan informasi yang ada pada soal, kita coba gunakan perbandingan sisi yang bersesuaian pada segitiga.
Kita misalkan lebar sungai adalah $x$ dan posisi pohon adalah $P$.
Dengan demikian kita peroleh 2 segitiga yang sebangun yaitu $\bigtriangleup ABP$ dan $\bigtriangleup DCP$.
$ \begin{array}
& \frac{AB}{DC} =\frac{AP}{DP} \\
& \frac{8}{6} = \frac{4+x}{x} \\
& 8x = 6(4+x) \\
& 8x = 24+6x \\
& 8x-6x = 24 \\
& 2x = 24 \\
& x = \frac{24}{2} \\
& x = 12
\end{array} $
$\therefore$ Pilihan yang sesuai adalah $(B)\ 12\ m$
10. Soal Seleksi Akademik YASOP SMAN 2 Balige 2005 |*Soal Lengkap
Suatu pohon yang tingginya $24\ m$ mempunyai bayangan di tanah sepanjang $18\ m$. Jika pohon pinus yang tinginya $60\ m$, maka bayangannya di tanah sepanjang...
$\begin{align}
(A)\ & 40\ m \\ (B)\ & 45\ m \\ (C)\ & 75\ m \\ (D)\ & 80\ m
\end{align}$
Alternatif Pembahasan:
Dengan menggunakan konsep perbandingan senilai maka kita peroleh:
$\begin{align}
\dfrac{t_{pohon}}{t_{pinus}} & = \dfrac{bayangan_{pohon}}{bayangan_{pinus}} \\
\dfrac{24}{60} & = \dfrac{18}{bayangan_{pinus}} \\
bayangan_{pinus} \times 24 & = 18 \times 60 \\
bayangan_{pinus} & = \dfrac{18 \times 60}{24} \\
bayangan_{pinus} & = 45
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(C)\ 45\ m$
11. Soal Seleksi Akademik YASOP SMAN 2 Balige 2005 |*Soal Lengkap
Segitiga $ABC$ seperti pada gambar di bawah ini:
$DE$ sejajar $AB$
$AB=5$, $DE=3$, $CE=x$ dan $EB=y$.
Perbandingan $x:y=\cdots$
$\begin{align}
(A)\ & 5:4 \\ (B)\ & 3:4 \\ (C)\ & 2:3 \\ (D)\ & 3:2
\end{align}$
Show
Dari gambar kita peroleh informasi bahwa $\bigtriangleup CDE$ sebangun dengan $\bigtriangleup CAB$ sehingga berlaku:
$\begin{align}
\dfrac{DE}{AB} & = \dfrac{CE}{CB} \\
\dfrac{3}{5} & = \dfrac{x}{x+y} \\
3(x+y) & = 5x \\
3x+3y & = 5x \\
3y & = 5x-3x \\
3y & = 2x \\
\dfrac{x}{y} & = \dfrac{3}{2}
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 3:2$
Jika engkau tidak sanggup menahan lelahnya belajar, Maka engkau harus menanggung pahitnya kebodohan ___pythagoras
Table
Tabel pada tema ini sudah disetting responsive, sebagai contoh jika jumlah kolom atau lebar tabel melebihi lebar layar maka agar tidak merusak layoutnya secara otomatis table akan memiliki fungsi scroll.
Silahkan buka artikel ini pada perangkat seluler anda dan sorot bagian tabel dibawah:
| No | Column_1 | Column_2 | Column_3 | Column_4 | Column_5 |
|---|---|---|---|---|---|
| 1 | Data_table_1 | 00.000.000 | 0.000.000 | 0.000.000 | 0.000.000 |
| 2 | Data_table_2 | 00.000.000 | 0.000.000 | 0.000.000 | 0.000.000 |
| 3 | Data_table_3 | 00.000.000 | 0.000.000 | 0.000.000 | 0.000.000 |
| 4 | Data_table_4 | 00.000.000 | 0.000.000 | 0.000.000 | 0.000.000 |
Untuk segala sesuatu hal yang perlu kita diskusikan terkait Soal dan Pembahasan Kesebangunan Dan Kekongruenan Matematika SMP silahkan disampaikan 🙏 CMIIW😊.
Jangan Lupa Untuk Berbagi 🙏 Share is Caring 👀 dan JADIKAN HARI INI LUAR BIASA! - WITH GOD ALL THINGS ARE POSSIBLE😊



















